Early epoch data for the Kālacakra calendar tradition
This article looks at a selection of the older epoch data for the Kālacakra karaṇa calendar system. The original epoch for the Kālacakra Tantra calendar is 23 March 806 CE. There will be more about this epoch at the end of this article.
After the tantra itself, the next readily available text quoting an epoch for the Kālacakra calendar is the Kālacakrāvatāra (dus kyi 'khor lo la 'jug pa), by Abhayākaragupta ('jigs med 'byung gnas sbas pa). Although this adds little of interest from an epoch point of view, it is nevertheless an extremely important work, being written by a major Kālacakra expert and having a Sanskrit original still preserved – in the Asiatic Society in Calcutta, India. This text uses an epoch of 1087 CE., but simply calculates the number of years back to the Tantra epoch in 806 CE.; it then uses the epoch data from the tantra.
Then there is a set of three short Indian texts that were written by Śākya Śrībhadra. These three texts are:
Śrī-kālacakragaṇ(an)opadeśa (dpal dus kyi 'khor lo'i rtsis kyi man ngag). This gives the calculations for the main structure of the calendar, the five components (pañcāṅga, yan lag lnga), which depend upon the weekday, anomaly and solar longitude.
(nyi zla 'dzin pa'i rtsis, Sanskrit title not given). This gives the calculation for the longitude of the Moon's nodes and a very brief discussion of the occurrence of eclipses.
Pañcagrahapṛthaggaṇanopadeśa (gza' lnga so so'i rtsis kyi man ngag). This gives the calculations for the longitudes of the five planets.
Śākya Śrībhadra has clearly adjusted the values for the weekday and solar longitude from those given in the tantra, presumably in the light of observation. He has also adjusted the data for Venus. The following is a translation of his calculations for the true month, weekday, anomaly and mean solar longitude. This and other translations in this article are fairly loose; translating properly would entail using the symbolic names that are used for numbers, such as eye (mig) for 2 and season (dus) for six. As the intention here is to explain the calculations rather than produce a literary work, these have all been replaced by the numbers concerned. All the calculations in the texts that are used in this article follow the style of the methods given in the Kālacakra Tantra and Vimalaprabhā – for an example of a full set of these calculations, see this page. In the following, the Tibetan is given ahead of the translation and explanation, and indented:
- stong pa rab skyes nas gzung ste // 'das lo byin pas lo dag pa'o // nyi mas bsgyur bas zla bar 'gyur // dgun zla 'bring sogs 'das zla sbyin // gnas gnyis 'og ma mig gis bsgyur // mda' ros thob la gcig bsres te // steng la byin pas zla dag 'gyur //
| Indian seasonal names for the months together with the sign the Sun enters during the month. The first column | ||
| Phālguna, dbo | Early-spring | Pisces |
| Caitra, nag pa | Mid-spring | Aries |
| Vaiśākha, sa ga | Late-Spring | Taurus |
| Jyeṣṭha, snron | Early-summer | Gemini |
| Āṣāḍha, chu stod | Mid-summer | Cancer |
| Śrāvaṇa, gro bzhin | Late-summer | Leo |
| Bhādrapada, khrums | Early-autumn | Virgo |
| Āśvina, tha skar | Mid-autumn | Libra |
| Kārtikka, smin drug | Late-autumn | Scorpio |
| Mārgaśīrṣa, mgo | Early-winter | Sagittarius |
| Pauṣa, rgyal | Mid-winter | Capricorn |
| Māgha, mchu | Late-winter | Aquarius |
"The true count of years is from 1206 CE. Multiply this by 12 to derive months and add the months since mid-winter (Pauṣa, rgyal). Write in two places and multiply the lower by 2; divide by 65 and add 1 to the quotient and then add this to the upper figure to derive the true month."
There are a couple of curious points about this calculation, which can be represented:
- m × 1;2 + 1;0
He adds no epoch value for the intercalation index, and yet does add 1 to the true month count. This is very unusual, so why not simply start a month earlier? A first assumption could be that he is simply using the tantra epoch data calculated forwards. Data to match his epoch has been added to the latest version of the open source software, KCK. Using that software we can see that if he is using the tantra data, then the epoch month immediately follows an intercalary month of Kārtikka. So, taking his initial epoch as Pauṣa, he then works back one month to the intercalary month of Mārgaśīrṣa. He seems simply to be using the tantra 806 epoch, without any correction. If he had corrected the data, the intercalary should be a few months later; based on the mean solar longitude of the Sun at the epoch new Moon (see discussion of this here), the intercalation index at his epoch should be 49 rather than zero. But this does not explain why he adds 1 to the true month calculation, instead of starting a month earlier.
Another possible explanation is that he wants the month of Pauṣa to be the second of two months that have an intercalation index of zero – an intercalary month and the month following it have the same intercalation index, either 0 or 1. If this is the case, then the "real" epoch month is actually an intercalary month of Mārgaśīrṣa. So, taking his initial epoch as an easily describable Pauṣa, he then works back one month to the intercalary Mārgaśīrṣa. This may have been done to avoid possible confusion if he had stated "add the months since early-winter (Mārgaśīrṣa, mgo)", as there were two of these. This represents a small difference from the tantra calculation, and is my preferred explanation – the tantra calculations have Kārtikka as the intercalary and give the month of Pauṣa an intercalation index of 2, which would not result from the calculations given here.
- zla dag gnas gsum bar ma la // so yis bsgyur te mig gis bsre // 'og la ros thob bar ma sbyang // lhag la mkha' sbyin bar nas gcig // 'og tu phab la drug cus bsgyur // mkha' byin des phri lhag chu srang // bar ma drug cus bgos thob rnams // steng byin lhag ma chu tshod gnas // de la ris bgos lhag gza' gnas //
"Write the true month in three places, multiply the middle by 32 and add 2. Divide the lower by 6 and subtract the quotient from the middle. Add a zero to the remainder (ie. multiply it by 10) and carrying 1 from the middle line to the lower, multiply it by 60 and subtract the number to which a zero has been added; the result is pala. Divide the middle by 60 and add the quotient to the top line, the remaider being nāḍī; divide the top by 7 and the remainder is the weekday."
This calculation is straightforward. If we consider the true month count to be zero (counting from the "real" epoch of Mārgaśīrṣa) we get:
- 0 -> 0
- 0 × 32 = 0 + 2 – 0 = 2
- 0 ÷ 6 = 0 rem. 0
This gives an epoch value of 0;2,0 (this is Saturday 2 December 1206.) Calculating from the tantra epoch to this new Moon would yield: 6;56,0. If we consider his stated epoch of the month of Pauṣa:
- 1
- 1 × 32 = 32 + 2 – 0 = 34 – 1 = 33
- 1 ÷ 6 = 0 rem. 1; 60 – 10 = 50
This gives an epoch value of: 1;33,50. Calculating from the tantra would give: 1;27,50.
- gnas gnyis 'og mar klu mig sbyin // dus gnyis (should be "nyi") bgos lhag cha shas gnas // nor la ri dang zla bsres te // steng ma lag pas bsgyur la gzhug // klu lag bgos lhag ril po'i gnas //
"Again two places, to the lower add 28 and divide by 126; the remainder is the fractional part; add the quotient and 17 to the top after multiplying it by 2. Divide by 28 and the remainder is the anomaly."
This is also straightforward, and gives an epoch value (Mārgaśīrṣa) for the anomaly of 17:28. The tantra calculations produce the same result.
- zla ba dag pa gdengs ka sbyin // gnas gsum bar ma drag pos bsgyur // 'og ma bu ga yon tan gyis // thob pas bar sbyang lhag ma la // mkha' dus bsgyur te thob pa dang // lhag ma drug gis bsgyur te thob // bar mas 'og phab rim sbyangs pa'i // lhag ma chu srang dbugs su gnas // dbus ma drug cus bgos pa'i lhag // chu tshod yin te thob pa la // gcig bsres steng ma lhag (should be "lag") bsgyur gzhug // de skar bgos lhag skar ma'i gnas //
"Add 8 to the true month, write in three places and multiply the middle by 11. Divide the bottom by 39 and subtract the quotient from the middle; multiply the remainder by 60 and divide again, multiplying the remainder by 6. Carry 1 from the middle, and subtract the remainders for pala and breaths. Divide the middle by 60 and the remainder is nāḍī; add 1 to the quotient and then add to the top multiplied by 2; divide by 27 and the remainder is mansions."
This is not quite so straightforward. If we calculate for the Mārgaśīrṣa epoch, adding the value of 8, the calculation yields:
- 8 × 2 = 16 + (1 + 1) = 18
- 8 × 11 = 88 – 1 = 87 ÷ 60 = 1 rem. 27
- 8 ÷ 39 = 0 rem. 8; 8 × 60 = 480 ÷ 39 = 12 rem. 12; 60 – 12 = 48 – 1 = 47
- 12 × 6 = 72, ÷ 39 = 1 rem 33; 6 – 1 – 1 = 4
- 33 × 13 = 429 ÷ 39 = 11; 13 – 11 = 2
The epoch value is therefore: 18;27,47,4,2. Calculating from the tantra epoch gives: 18;26,55,2,4.
Why does he add 8 to the month count? This takes the calculations back to the new Moon (Sunday 9 April 1206) at the beginning of the month of Vaiśākha. As his data give the mean solar longitude at that new Moon as 1;0,0,0,0, perhaps this was done to simplify the calculations.
The next epoch data he gives, in the second text mentioned above, is for Rāhu; this is 18, the same value as would be derived from the original tantra calculation. In the third text he gives the calculations for the planets, and starts off by again counting back 8 months before establishing his count of days. The epoch data he gives for the planets are therefore for the new Moon at the beginning of the month of Vaiśākha. These data are:
These are all the same as would be calculated from the tantra, with the exception of the figure of 1071 for Venus. The tantra calculations would give 546. There is clearly a major error in the original tantra data for Venus, and we probably have here an attempt to correct for this. However, it was not successful – the figure of 1071 translates to a mean heliocentric longitude of Venus of 171.6°, but the actual mean longitude was 348.9°.
Early Tibetan epoch data
A couple of very early sets of epoch data are given in Tibetan texts by Chogyal Phakpa (chos rgyal 'phags pa). These are interesting due to his importance in the development of the Tibetan tradition, having introduced the system of numbering the lunar months that is still in use today, and also because these data have partly been discussed and interpreted wrongly by Zuihō Yamaguchi ("The Significance of Intercalary Constants in the Tibetan Calendar and Historical Tables of Intercalary Months"). He maintains that the karaṇa calculations were adjusted "on the basis of ... observations of the winter solstice" and that this involved the introduction of a figure of 7 in the intercalation index. He claims that "this constant of '7' is held to be an oral teaching or even a secret teaching (man ngag)." As evidence of this, he refers to texts by Chogyal Phakpa, and translations from these texts are given here.
The first of these texts is the "lnga bsus sgra gcan gza' lnga dang bcas pa'i rtsis gzhi. The following translations are similar to those above, covering the true month, weekday, anomaly and solar longitude:
- bsil zer can la zhi ba sogs // 'das pa bsres pa lo dag yin // nyi mas bsgyur la nag sogs sbyin // gnas gnyis 'og ma mig gis bsgyur // 'dod sbyin mda' ros rnyed steng bsre // gnyis 'phel shol yin lhag ma ni // mig gis rnyed pas 'das pa rtogs //
"Take the years, Saumya, etc., elapsed since 1248 as the true year; multiply by 12 and add the months since Caitra; write in two places and multiply the bottom by 2, add 13 and divide by 65, adding the quotient to the top; when this increases by 2 there is an intercalary; divide the remainder by 2 to determine the months passed (since the last intercalary)."
This intercalation index of 13 divided by 2 is refered to by Yamaguchi as 6.5. But this is nothing special. It is simply calculated forward from the original tantra epoch, and no change has been introduced. This is easy to check. This text has an epoch year of 1248. So, counting years from the Kālacakra epoch of 806, and then multiplying by 12 and again by 2, we get:
- ( 1248 – 806 ) × 12 × 2 = 10608
There is no epoch value given in the tantra for the intercalation index, so, nothing to add; next, divide by 65:
- 10608 ÷ 65 = 163 rem. 13
Divided by 2, this is the figure that Yamaguchi quotes. The text itself gives the figure as 13, for a division by 65; Yamaguchi quotes 6.5 for a division by 32.5 – these are equivalent. In the present example, the epoch value is added after the month value on the lower line has been multiplied by 2; in the example that follows, the epoch value is added before the multiplication. Yamaguchi also states that the author does not "allude to any initial standard year or standard years, but since these were to be found in the bsDus rgyud and 'Grel chen, they were a matter of common knowledge..." This is not the case, and Chogyal Phakpa is using as epoch the year 1248.
- steng gi zla dag gnas gsum gzhag // dbus su mig sbyin so yis bsgyur // rtsa bar gcig bsre dus kyis bgo // lhag ma thig les brgyan pa yi // steng nas gcig phab drug cu la // sbyangs lhag gza' yi chu srang yin // thob la gzugs bsre dbus su sbyangs // drug cus bgos lhag chu tshod do // nor la bzhi bsre steng du sbyin // thub pas bgos pa'i lhag ma gza' //
"(For the weekday:) take the upper true month and write in three places; add 2 to the middle and multiply by 32; add 1 on the bottom and divide by 6; add a zero to the remainder (ie. multiply by 10) and carrying one from the middle line, subtract from 60 – the result is the weekday pala; add 1 to the quotient and subtract from the middle; divide by 60 and the remainder is nāḍī; add 4 to the quotient and add to the top; divide by 7 and the remainder is the weekday."
Taking a true month count of zero:
- 0 + ( 1 + 4 ) = ÷ 7 = 0 rem. 5
- 0 + 2 × 32 = 64; 63 – ( 0 + 1 ) = 62 ÷ 60 = 1 rem. 2
- 0 + 1 ÷ 6 = 0 rem. 1; 60 – 10 = 50
Epoch value is 5;2,50 (Thursday 5 March 1248).
- zla dag gnas gnyis 'og ma la // zla ba mi bdag rnams bsres nas // dus nyis bgos lhag cha shas yin // steng la me bsre mig gis bsgyur // thob pa byin la klu lag gis // bgos pa'i lhag ma tshogs su 'gyur //
"(For the anomaly:) write the true month in two places and add to the bottom 161 (yes, really!); divide by 126 and the remainder is the fractional part; add 3 to the top and multiply by 2 and then add the lower quotient and divide by 28; the remainder is the anomaly."
Taking the true month as zero again:
- 0 + 3 × 2 = 6 + 1 = 7 ÷ 28 = 0 rem. 7
- 0 + 161 = 161 ÷ 126 = 1 rem. 35
Epoch value is: 7;35
- gnas gsum dbus ma drag pos bsgyur // rtsa bar bdun bsre so dgus dbye // lhag ma mkha' ros bsgyur ba la // so dgus phye la rnyed pa des // steng nas gcig phab drug cu la // sbyangs lhag skar ma'i chu srang yin // thob pa gong mar mda' bsres pas // dbus su sbyang bzhin (zhing?) drug cus bgo // lhag ma chu tshod steng ma ni // mig gis bsgyur la thob pa bsre // 'khor los bgos lhag skar ma'o //
"(For the Sun:) write the true month in three places and multiply the middle by 11; on the bottom, add 7 and divide by 39; multiply the remainder by 60, divide by 39 and subtract the quotient from 60, carrying 1 from above; the remainder is pala; take the earlier quotient, add 5, and then subtract from the middle; divide by 60 and the remainder is nāḍī; multiply the top figure by 2 and then add the quotient from the middle; divide the result by 27 and the remainder is mansions."
Taking the true month as zero again:
- 0 × 2 = 0 –1 = 26
- 0 × 11 = 0 – 1 = –1 – ( 0 + 5 ) = – 6 => 54 ÷ 60 = 0 rem. 54
- 0 + 7 = 7 ÷ 39 = 0 rem. 7; 7 × 60 = 420 ÷ 39 = 10 rem. 30; 60 – 10 = 50 – 1 = 49
Not described in the text, but, carrying down for breaths and final (13) fractional part:
- 30 × 6 = 180, ÷ 39 = 4 rem 24; 6 – 4 – 1 = 1
- 24 × 13 = 312 ÷ 39 = 8; 13 – 8 = 5
This gives an epoch value of 26;54,49,1,5
All these epoch data are precisely those that would be derived by taking the original epoch data in the tantra and calculating forwards to Chogyal Phakpa's epoch of Thursday 5 March 1248 – nothing has been changed or added. Anybody interested in checking all these data for themselves could use the open source software KCK, that is available here.
The next text by the same author is the "dpal dus kyi 'khor lo'i rtsis dus gsal ba'i sgron me". Yamaguchi quotes this text next (although he mistakenly gives it the name of the very short text that precedes it) and indicates the intercalation index of 7:
- nam mkha'i dbyings su rab byung sogs // 'das pa bsres pa lo dag yin // nyi mas bsgyur la nag sogs sbyin // gnas gnyis 'og mar ri bsres la // mig gis bsgyur la mda' ro yis // rnyed pa steng byin zla dag yin // lhag ma mig gis rnyed pa yis // 'das pa'i zla lhag nam byung brtag // sum cu gnyis gsum spel 'byung bas // mo 'ongs pa ni shugs las shes //
"The years elapsed since prabhava (1267) are the true year. Multiply by 12 and add the months since Caitra. Write in two places; add 7 to the lower value, multiply by two and then divide by 65. Add the quotient to the upper figure to find the true month; divide the remainder by 2 to yield the months since the last intercalary; after 32 or 33 there will be another."
Here is the epoch value of 7, and again, this is easily calculated from the data in the tantra. The epoch for this text is the year 1267, and he essentially divides by 32.5, so we should do the same (the epoch value is added before multiplication by 2):
- ( 1267 – 806 ) x 12 = 5532
- 5532 ÷ 32.5 = 170 rem. 7
Again, this is easily calculated from the tantra epoch, and there is nothing special going on – no changes to the intercalation constants, as Yamaguchi suggests, no "secret teaching".
- zla ba dag pa gnas gsum gzhag // dbus su gzugs bsre so yis bsgyur // de la nyi ma rnam par sbyin // 'og tu mig bsre dus kyis bgo // lhag ma phyogs kyis bsgyur ba yis // steng nas gcig phab drug cu la // sbyangs lhag gza' yi chu srang yin // thob pas dbus sbyang drug cus bgo // lhag ma chu tshod rnyed steng gzhug // thub pas bgos pa'i lhag ma gza' //
"(For the weekday:) write the true month in three places; add 1 to the middle and multiply by 32, then add 12; add 2 to the bottom figure and divide by 6. Multiply the remainder by 10, carry 60 from the middle line, and subtract from this; the result is the weekday pala; subtract the quotient from the middle and divide by 60; the remainder is the count of nāḍī, and the quotient is added to the top, which is then divided by 7, the remainder being the weekday."
M as zero:
- M + 0 = 0
- M + 1 = 1 × 32 = 32 + 12 = 44 – 1 = 43 – 0 = 43
- M + 2 = 2 ÷ 6 = 0 rem. 2; 60 – 20 = 40
The epoch value is 0;43,40 (Sunday 27 March 1267)
- gnas gnyis 'og mar nor zla sbyin // dus nyis bgos lhag cha shas yin // steng ma mig gis bsgyur ba la // nor la me bsres sbyin par bya // klu lag gis phye'i lhag ma tshogs //
"(For the anomaly:) write the true month in two places and add 18 to the lower and divide by 126; the remainder is the fractional part; multiply the upper value by 2, and add the (lower) quotient after adding 3; divide by 28 and the remainder is the anomaly."
M as zero:
- M × 2 + ( 0 + 3 ) = 3
- M + 18 = 18 ÷ 126 = 0 rem. 18
The epoch value is 3;18
- slar yang zla dag gnas gsum gzhag // dbus ma drag pos bsgyur bar bya // 'og tu nor sbyin so dgus dbye // lhag ma mkha' ros bsgyur ba la // so dgus phye la thob pa yis // steng nas gcig phab mkha' dus la // sbyangs lhag skar ma'i chu srang yin // rnyed pa snga mar ro bsres pas // dbus la sbyangs nas drug cus bgo // lhag ma chu tshod steng ma yin // mig gis bsgyur la rnyed pa gzhug // 'khor los bgos lhag skar ma ste // dhru ba rnam par dag pa'o //
"(For the Sun:) again, write the true month in three places and multiply the middle by 11; add 8 to the bottom line and divide by 39; multiply the result by 60; divide by 39, and take the remainder and subtract it from 60 carried from the middle line, the result being pala; the earlier quotient has 6 added, and the result subtracted from the middle; divide by 60 and the remainder is nāḍī; multiply the upper line by 2 and then add the quotient; divide by 27 and the result is mansions, this is the true longitude."
- 0 × 2 = 0 – 1 = 26
- 0 × 11 = 0 –1 – ( 0 + 6 ) = 60 – 7 = 53
- 0 + 8 = 8 ÷ 39 = 0 rem. 8; 8 × 60 = 480 ÷ 39 = 12 rem. 12; 60 – 12 = 48 – 1 = 47
Again, not described in the text, but carrying down for breaths and final (13) fractional part:
- 12 × 6 = 72 ÷ 39 = 1 rem 33; 6 – 1 – 1 = 4
- 33 × 13 = 429 ÷ 39 = 11; 13 – 11 = 2
The epoch value is: 26;53,47,4,2
Again, all these data are exactly as would be derived when calculating forwards from the data in the Kālacakra Tantra.
Yamaguchi's next reference is to the text called "rtsis dus gsal ba'i sgron me'i don yang dag par bsdus pa". As its name suggests, this is simply a synopsis of the previous one and naturally uses the same data. The next text by Chogyal Phakpa that Yamaguchi references is the "rtsis kyi gtsug lag dang mthun par nges pa". Yamaguchi claims that this adds a value of 14 (double 7) as the intercalation constant. However, he has misread the text, and it actually adds 17 (thub pa zla ba), which is then doubled anyway, to give an intercalation index of 34.
Association of the months (Indian names) with the Chinese month numbers, and seasonal and animal names, according to Drakpa Gyaltsen (grags pa rgyal mtshan):
| Māgha | 1 | Early-spring | Tiger |
| Phālguna | 2 | Mid-spring | Rabbit |
| Caitra | 3 | Late-Spring | Dragon |
| Vaiśākha | 4 | Early-summer | Snake |
| Jyeṣṭha | 5 | Mid-summer | Horse |
| Āṣāḍha | 6 | Late-summer | Sheep |
| Śrāvaṇa | 7 | Early-autumn | Monkey |
| Bhādrapada | 8 | Mid-autumn | Bird |
| Āśvina | 9 | Late-autumn | Dog |
| Kārtikka | 10 | Early-winter | Pig |
| Mārgaśīrṣa | 11 | Mid-winter | Mouse |
| Pauṣa | 12 | Late-winter | Ox |
This latter text by Chogyal Phakpa is certainly interesting, as it is said to express the Chinese method of determining months and years. All such works start with a homage to some deity or personage, and this one addresses Mañjugoṣa, considered to have revealed the Chinese calendrical system. Towards the end of the text Chogyal Phakpa states that the 60-year cycle of years starts in India with Prabhava (eg. 1267) whereas in China the cycle starts with the wood-mouse year (eg. 1264). He continues by describing the difference in the month that is considered to start the year: in Sambhala, the first month is Caitra but in China it is Pauṣa – three months earlier. This is considered in China to be the early-spring month and is called "the first". He tells us that in this text he has shown how to derive the years and months according to the Chinese system, but using the methods of Kālacakra. He states that in Tibet it is taught that the Chinese calculations are in error, and so he has written this little text to show the compatibilities between the Chinese and Kālacakra systems.
The calculations that he gives are certainly in exactly the same Kālacakra style as those earlier in this article, and yield the same results as the standard Kālacakra system for his epoch day. The only differences are that he starts the calculation from "the first" month of a wood-mouse year, and he has a different intercalation index.
- His epoch is: Wednesday 30 January 1264.
- Mean weekday: 4;2,10
- Anomaly: 34;105
- Mean Sun: 22;45,47,4,2
- Rāhu: 35
It is possible that I have misunderstood something here, but given that his intercalation index for the epoch day is 34, this makes the next intercalary month just over a year later, Vaiśākha, starting on 17 May 1265. However, during this month the Sun entered Gemini, and so it should not be an intercalary. Also, his epoch new Moon is at the start of the month Māgha, one after Pauṣa. Perhaps the naming convention is different here, or there is a simple mistake in the text – see the table; I suspect the text should read that the first month in China is Māgha, not Pauṣa. Whatever name the month should have, I have not yet been able to understand why he has this value of 34 for the intercalation index, and so for now, at least, we'll have to leave this there.
The epoch of the Kālacakra Tantra
| On astronomy and chronology: In his interesting paper entitled "Remarks on the Origin of |
Yamaguchi has unfortunately misunderstood these texts, and his arguments regarding modification to the intercalation constants lead him to the remarkable conclusion that, regarding the epoch of the Kālacakra Tantra, "it was not the 1st day of the 3rd month of the hor zla in 806 but the 16th day of the 1st month of 803 that was identified as the start of the initial standard year, and that the sun was considered to have reached the vernal equinoctial point on this date." Although most do agree with 806, Yamaguchi is not alone in being confused about the identification of the Kālacakra epoch, and so it is worth taking a look at this properly. Like many other writers (see the box), Yamaguchi fails to consider the astronomy involved, even though the data in the Kālacakra Tantra are for the construction of a calendar, and give us epoch values for the mean longitudes of the Sun, Mercury, Venus, Mars, Jupiter, Saturn and the Moon's node (at new Moon, the Moon has the same longitude as the Sun). So, the question to ask is if this represents a fair picture of the sky at any time, and when?
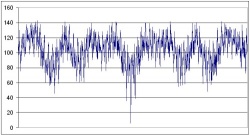
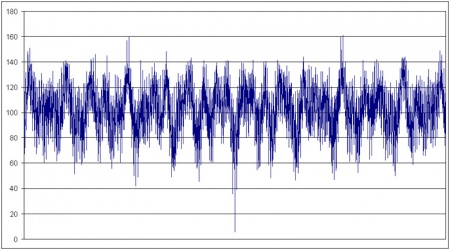
Perhaps the best way to illustrate this is pictorially. Given the set of data for the mean longitudes in the tantra, we can then calculate the actual mean positions for other new Moons either side of, and including, the 806 epoch. As an indicator of error, we can take the root mean square (RMS) of the differences between the Kālacakra epoch data and the mean longitudes calculated using modern astronomy (using the formulae in Astronomical Algorithms, by Jean Meeus). This gives us a single number index of accuracy, and larger values of this RMS figure indicate greater divergence from the tantra figures. The following chart gives the RMS figures for new Moons, three years either side of the 23 March 806 (mean) new Moon.
The lowest point, with an RMS value of 5.81, is the 23 March 806 new Moon, which is clearly the best fit to the Kālacakra data by a very long way; it is, in fact, the only reasonable fit. If we were to take into consideration the possibility that the original data were based on an early sidereal zodiac intended to be corrected to equatorial, the match would in fact be closer. And so what of Yamaguchi's proposed epoch of the beginning of "the 16th day of the 1st month of 803" (11 January 803)? Not only does the RMS come out at a high value of 78.08 (any correlation with the tantra data is effectively random), but the Sun is nowhere near the equinoctial point, having a longitude of 295° – in Capricorn!
In an analysis like this we are bound to see peaks and troughs when planets complete their cycles. For example, the two troughs just dipping below 40 in the above chart are times when the mean longitudes of the Sun, Mercury and Mars again come reasonably close to the values in the tantra. (I should point out that in these calculations I have corrected an obvious error in the tantra data for Venus – but using the original data makes little and no significant difference to the results.)
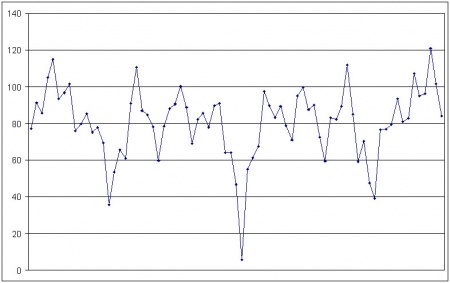
But, have we looked far enough? The following chart shows the same data, but now 50 years either side of the March 806 new Moon.
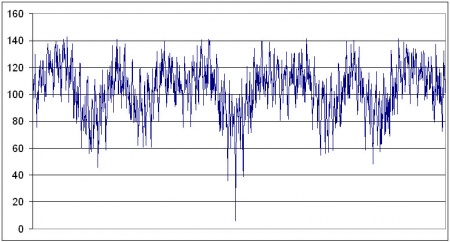
And for good measure, 200 years either side:
E. Henning